[最も欲しかった] つるかめ 算 例題 427573

特殊算 つるかめ算の解き方 私立中学受験 高校受験対策のプロ家庭教師ふなきち

つるかめ算の基本問題 問題1 つるとかめが合わせて9ひきいます。足の数は合わせて26本です。つるとかめはそれぞれ何びきいますか。 → 解答 問題2 1円玉と5円玉が合わせて28枚あり、その合計金額もっともっと 鶴亀算 つるかめ算 「例題」 8人ですると31日かかる仕事があります。 この仕事をはじめは8人全員で何日間かしました。 しかし、途中から2人が出張したため、6人で仕事をすることになり、34日で仕事を終えました。

つるかめ 算 例題

つるかめ 算 例題-2 つるとかめの数は、合計40、足の数は86本。 かめの数は？ 21 < 連立方程式 >; つるかめトンボ算も練習します。簡単に言えば3種類についてのつるかめ算です。中学入試でもよく出ます。 経過 09年8月23日 つるかめ算を作成しました。 11年5月23日 解説プリントの例題1に数値のまちがいがありましたので修正しました。30ではなく40

鶴亀算 Wikipedia

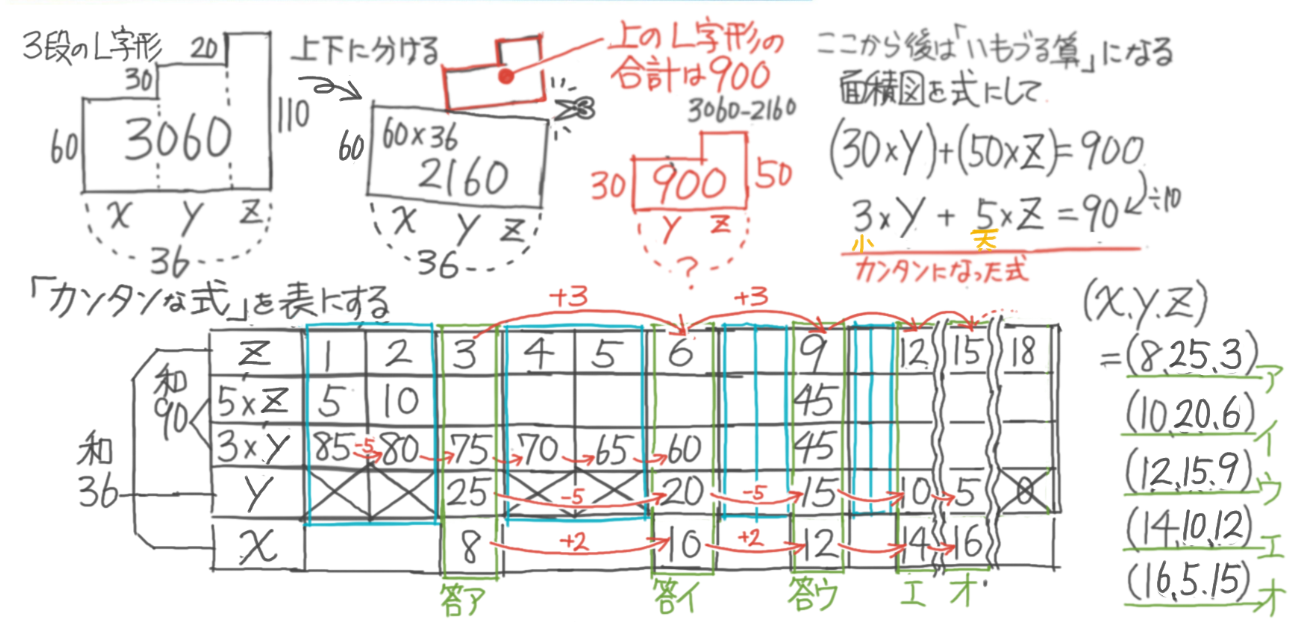
鶴亀算 つるかめ算 算数文章問題の鶴亀算（つるかめ算）とは、 例えば、鶴と亀の合計の数と、その足の合計の本数が分かっているとき、鶴と亀のそれぞれの数を求めるような問題を鶴亀算といいます。 「例題」 鶴・亀あわせて、頭数は10、足の数は32本 そのため、問題のなかに「2つのもの の 2つの合計」が出てきたら「つるかめ算」なのだと、自分で気がつく必要があります。 今回の例題でいうと、以下が「2つのもの の 2つの合計」にHello School 算数 つるかめ算 練習問題 解答と解説 インターネット上で受験算数の一通りの基本的解法をマスターしよう♪。

 つるかめ算とは？例題 もともとはツルとカメではなく、キジとウサギでした。 $3 世紀ごろの中国の算術書である「孫子算経(そんしさんけい)」において「雉兎同籠」という問題があり中学受験 算数の練習問題プリントです。栄光ゼミナールの約7万名の生徒が自宅や教室で毎日挑戦している問題データベースから、定番の問題を集めて公開しています。 中学受験 算数プリントの主な内容 和差算 植木算 周期算 分配算 方陣算 展開図と見取図 等差数列のしくみ 円と多角形 割合管理人 11月 8, 18 / 11月 27, 18 中学受験に出題される文章問題、 「つるかめ算」の問題集です。 問題をランダムで生成することができ、答えの表示・非表示も切り替えられます。 印刷してご活用ください。 ちなみにつるかめ算の基本や文章問題の解き

つるかめ 算 例題のギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

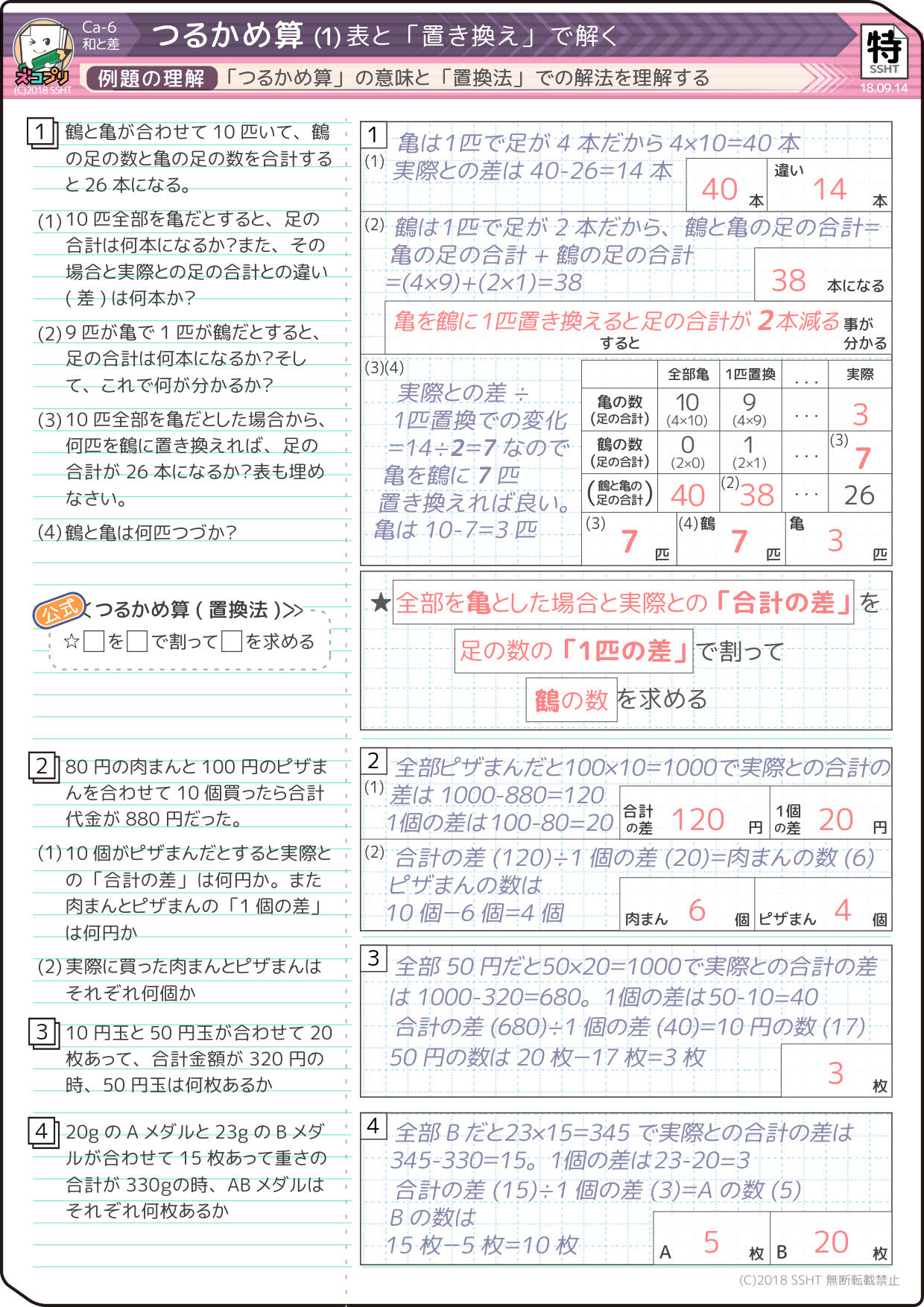
つるかめ算の解き方 2つの方法で解説 Umetopi	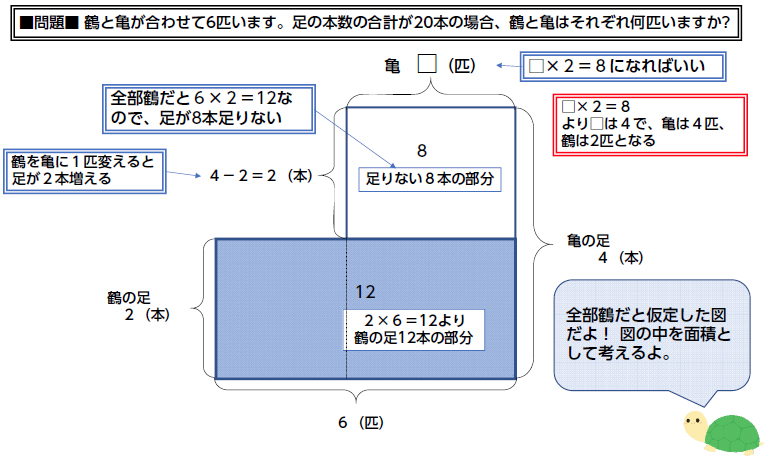つるかめ算の解き方 2つの方法で解説 Umetopi	つるかめ算の解き方 2つの方法で解説 Umetopi
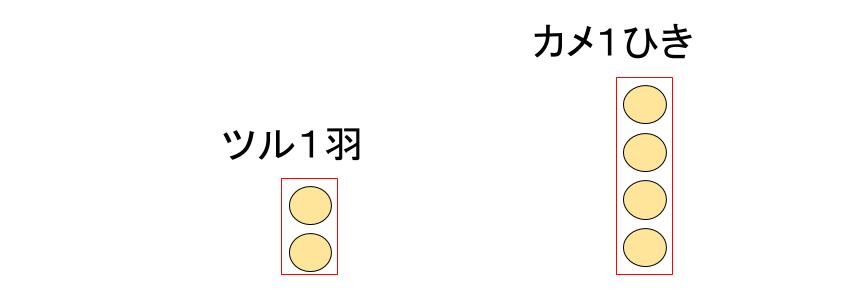つるかめ算の解き方 2つの方法で解説 Umetopi	つるかめ算の解き方 2つの方法で解説 Umetopi	つるかめ算の解き方 2つの方法で解説 Umetopi
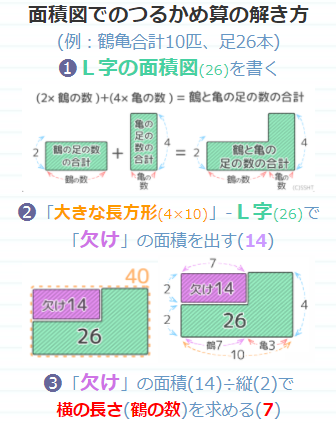つるかめ算の解き方 2つの方法で解説 Umetopi	つるかめ算の解き方 2つの方法で解説 Umetopi	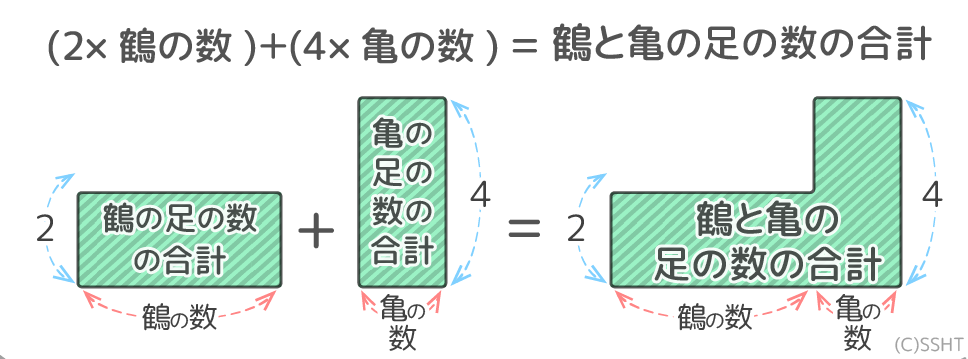つるかめ算の解き方 2つの方法で解説 Umetopi
つるかめ算の解き方 2つの方法で解説 Umetopi	つるかめ算の解き方 2つの方法で解説 Umetopi	つるかめ算の解き方 2つの方法で解説 Umetopi
つるかめ算の解き方 2つの方法で解説 Umetopi	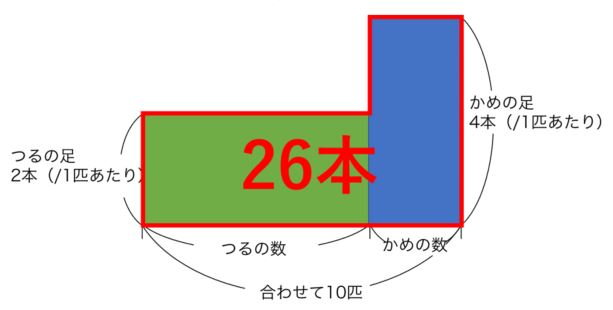つるかめ算の解き方 2つの方法で解説 Umetopi	つるかめ算の解き方 2つの方法で解説 Umetopi
つるかめ算の解き方 2つの方法で解説 Umetopi	つるかめ算の解き方 2つの方法で解説 Umetopi	つるかめ算の解き方 2つの方法で解説 Umetopi
つるかめ算の解き方 2つの方法で解説 Umetopi	つるかめ算の解き方 2つの方法で解説 Umetopi	つるかめ算の解き方 2つの方法で解説 Umetopi
つるかめ算の解き方 2つの方法で解説 Umetopi	つるかめ算の解き方 2つの方法で解説 Umetopi	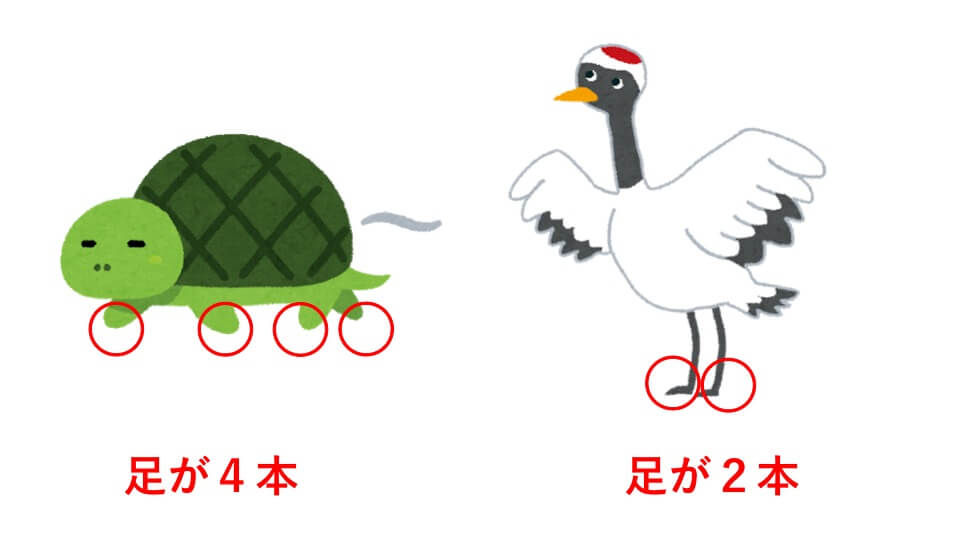つるかめ算の解き方 2つの方法で解説 Umetopi
つるかめ算の解き方 2つの方法で解説 Umetopi	つるかめ算の解き方 2つの方法で解説 Umetopi	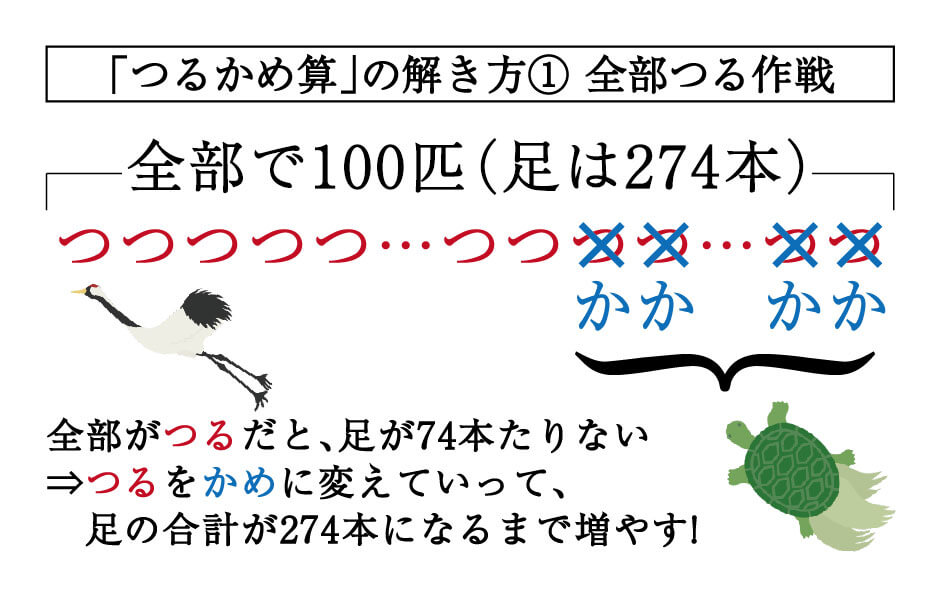つるかめ算の解き方 2つの方法で解説 Umetopi
つるかめ算の解き方 2つの方法で解説 Umetopi	つるかめ算の解き方 2つの方法で解説 Umetopi	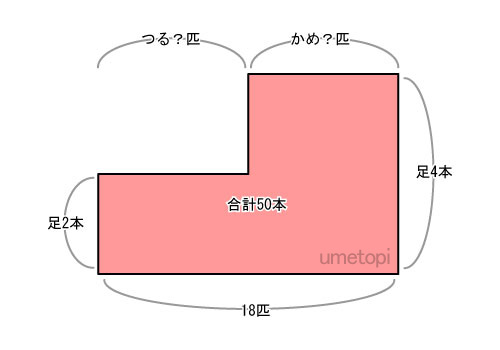つるかめ算の解き方 2つの方法で解説 Umetopi
つるかめ算の解き方 2つの方法で解説 Umetopi	つるかめ算の解き方 2つの方法で解説 Umetopi	つるかめ算の解き方 2つの方法で解説 Umetopi
つるかめ算の解き方 2つの方法で解説 Umetopi	つるかめ算の解き方 2つの方法で解説 Umetopi	つるかめ算の解き方 2つの方法で解説 Umetopi
つるかめ算の解き方 2つの方法で解説 Umetopi	つるかめ算の解き方 2つの方法で解説 Umetopi	つるかめ算の解き方 2つの方法で解説 Umetopi
つるかめ算の解き方 2つの方法で解説 Umetopi	つるかめ算の解き方 2つの方法で解説 Umetopi	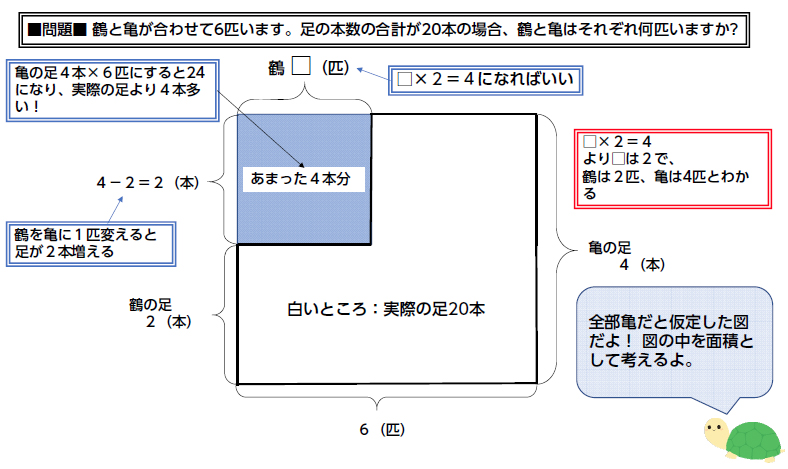つるかめ算の解き方 2つの方法で解説 Umetopi
つるかめ算の解き方 2つの方法で解説 Umetopi	つるかめ算の解き方 2つの方法で解説 Umetopi	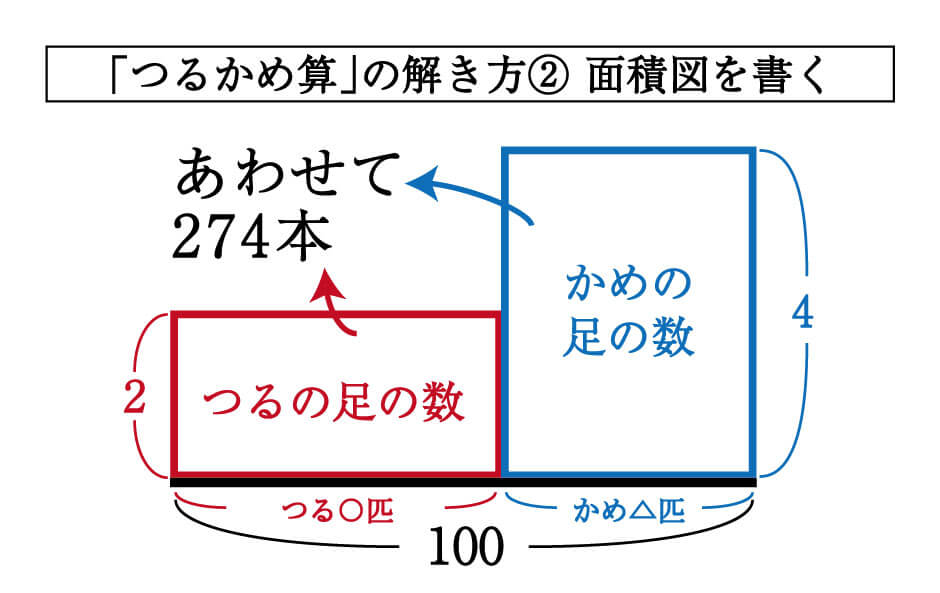つるかめ算の解き方 2つの方法で解説 Umetopi
つるかめ算の解き方 2つの方法で解説 Umetopi	つるかめ算の解き方 2つの方法で解説 Umetopi	つるかめ算の解き方 2つの方法で解説 Umetopi
つるかめ算の解き方 2つの方法で解説 Umetopi	つるかめ算の解き方 2つの方法で解説 Umetopi	つるかめ算の解き方 2つの方法で解説 Umetopi
つるかめ算の解き方 2つの方法で解説 Umetopi	つるかめ算の解き方 2つの方法で解説 Umetopi	つるかめ算の解き方 2つの方法で解説 Umetopi
つるかめ算の解き方 2つの方法で解説 Umetopi	つるかめ算の解き方 2つの方法で解説 Umetopi	つるかめ算の解き方 2つの方法で解説 Umetopi
つるかめ算の解き方 2つの方法で解説 Umetopi	つるかめ算の解き方 2つの方法で解説 Umetopi	つるかめ算の解き方 2つの方法で解説 Umetopi
つるかめ算の解き方 2つの方法で解説 Umetopi	つるかめ算の解き方 2つの方法で解説 Umetopi	つるかめ算の解き方 2つの方法で解説 Umetopi
つるかめ算の解き方 2つの方法で解説 Umetopi	つるかめ算の解き方 2つの方法で解説 Umetopi	つるかめ算の解き方 2つの方法で解説 Umetopi
つるかめ算の解き方 2つの方法で解説 Umetopi	つるかめ算の解き方 2つの方法で解説 Umetopi	つるかめ算の解き方 2つの方法で解説 Umetopi
つるかめ算の解き方 2つの方法で解説 Umetopi	つるかめ算の解き方 2つの方法で解説 Umetopi	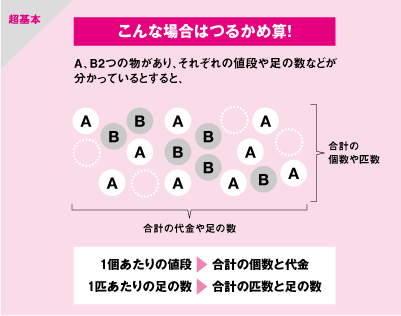つるかめ算の解き方 2つの方法で解説 Umetopi
つるかめ算の解き方 2つの方法で解説 Umetopi	つるかめ算の解き方 2つの方法で解説 Umetopi	つるかめ算の解き方 2つの方法で解説 Umetopi
つるかめ算の解き方 2つの方法で解説 Umetopi	つるかめ算の解き方 2つの方法で解説 Umetopi	つるかめ算の解き方 2つの方法で解説 Umetopi
つるかめ算の解き方 2つの方法で解説 Umetopi	つるかめ算の解き方 2つの方法で解説 Umetopi	つるかめ算の解き方 2つの方法で解説 Umetopi
つるかめ算の解き方 2つの方法で解説 Umetopi	つるかめ算の解き方 2つの方法で解説 Umetopi	つるかめ算の解き方 2つの方法で解説 Umetopi
つるかめ算の解き方 2つの方法で解説 Umetopi	つるかめ算の解き方 2つの方法で解説 Umetopi	つるかめ算の解き方 2つの方法で解説 Umetopi
つるかめ算の解き方 2つの方法で解説 Umetopi	つるかめ算の解き方 2つの方法で解説 Umetopi	つるかめ算の解き方 2つの方法で解説 Umetopi
つるかめ算の解き方 2つの方法で解説 Umetopi	つるかめ算の解き方 2つの方法で解説 Umetopi	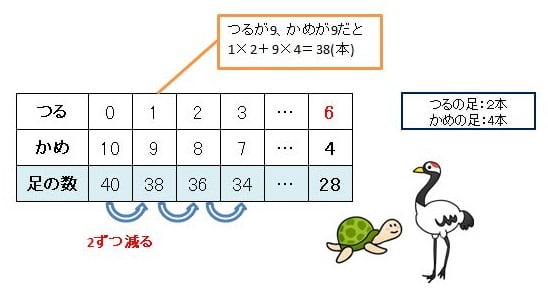つるかめ算の解き方 2つの方法で解説 Umetopi
つるかめ算の解き方 2つの方法で解説 Umetopi	つるかめ算の解き方 2つの方法で解説 Umetopi	つるかめ算の解き方 2つの方法で解説 Umetopi
つるかめ算の解き方 2つの方法で解説 Umetopi	つるかめ算の解き方 2つの方法で解説 Umetopi	つるかめ算の解き方 2つの方法で解説 Umetopi
つるかめ算の解き方 2つの方法で解説 Umetopi	つるかめ算の解き方 2つの方法で解説 Umetopi	つるかめ算の解き方 2つの方法で解説 Umetopi
つるかめ算の解き方 2つの方法で解説 Umetopi	つるかめ算の解き方 2つの方法で解説 Umetopi

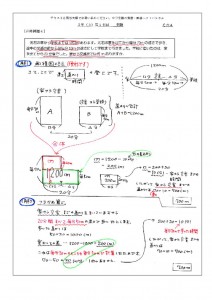
Hello School 算数 つるかめ算 インターネット上で受験算数の一通りの基本的解法をマスターしよう♪。 例題1 1本80円のえんぴつと1本100円のえんぴつを合わせて本買い、代金は1860円でした。 つるかめ算の基本的な例題と解き方 ツルとカメが 合わせて8匹 います。 足の数は合わせて26本 でした、ツルとカメはそれぞれ何匹いますか。ただし、ツルの足は2本、カメの足は4本です。 計算で解く方法